Mathematica worksheet 1

Intro

其他数学软件: MATLAB, Mathematica, Maple.

MATLAB, namely, Matrix Laboratory 矩阵实验室, 数值计算, 主要关注矩阵上的运算, 仿真. 在工程上运用广泛, 例如偏微分方程求解

Mathematica, 符号计算, 语言灵活, 非常适合数学系 (!)

Maple, 符号计算, 在早年时版本之间没有兼容性 (?), 有很多工具包

Resource

主要参考视频: https://www.bilibili.com/video/BV1av411N7Xi/

主要参考书: Mathematica Programming: An Advanced Introduction -- Leonid Shifrin, 部分中文翻译

j-star.org 笔者翻译了 worksheet1, 可以作为参考

Mathematica Stack Exchange

Mathematica 百度贴吧

MathCraft

Project Euler: 数学编程练习题网站, 部分解答

这是一个什么样的教程

本教程主要关注 Mathematica 核心语言, 要求有基本微积分和线性代数的知识以及一定的基本编程知识. 使用 Mathematica 这一工具的主要目的是提高工作效率, 效率的定义对不同专业的人是不同的, 对数学工作者来说, 最有效率的程序是 “开发时间” + “运行时间” 最小的程序, 数学工作者不必追求完美, 把运行时间缩到很短, 在跑程序的时候大可去煮一杯咖啡. 那么什么是 “数学工作者 (Mathematician)” ?

“数学家”在中文语义中通常指的是有卓越数学成就的人, 一般的数学工作者在英文中也称为 Mathematician. 在数学家圈子内部, 人们也认为 Mathematician 分成两个有代表性的群体:

用阳光和雨露吃核桃的人 v.s 用锤子和凿子吃核桃的人 -- A. Grothendieck, Récoltes et Semailles (收获与播种)

理论建设者 vs. 问题求解者 -- W.T. Gowers, The Two Cultures of Mathematician (2000)

我们把前一类称为 “数学家”, 后一类称为 “数学工作者”.

数学家的工作方式: 思考, 再思考, 画交换图表 (如果需要), 问题解决; 数学工作者的工作方式则是在选题后解决问题. 数学家一般不需要大量计算, 而数学工作者需要.

机器不能解决一切数学问题, 关键步骤由人来解决, 将机器的工作交给机器, 人的工作交给人是一种高效合理的工作方法.

关键问题在于怎么样将计算方法教给计算机, 参考 Curry-Howard correspondence.

充分理解我们所做的计算, 把它归结为 “重写规则” (尤其在 Mathematica 中)

将 “重写规则” 教给计算机, 使它帮助我们完成计算

基本操作

作为数学计算器的 Mathematica

简单的输入到输出: Shift + Enter 来输出:

worksheet1_1.png

worksheet1_2.png

NOTE: 如果你进行了一个比较奇怪的运算, 可以使用快捷键 Alt + . 来结束计算.

特殊数学符号例如: E, Pi, I, EulerGamma:

worksheet1_3.png

worksheet1_4.png

worksheet1_5.png

worksheet1_6.png

Mathematica 有高精度的数值计算, 注意 MATLAB 是数值计算软件, 但不关注高精度, 因为在工程上不会关注太高的位数:

worksheet1_7.png

worksheet1_8.png

初等代数运算

worksheet1_9.png

worksheet1_10.png

worksheet1_11.png

worksheet1_12.png

worksheet1_13.png

worksheet1_14.png

微积分运算

worksheet1_15.png

worksheet1_16.png

worksheet1_17.png

worksheet1_18.png

worksheet1_19.png

worksheet1_20.png

worksheet1_21.png

worksheet1_22.png

worksheet1_23.png

worksheet1_24.png

NOTE: Ctrl+ / 可以显示出分数线, 同理 Ctrl+ ^ 可以显示幂, 也可以在工具栏->面板->数学助手中查询
NOTE: 其中 -> 表示一个替换规则, 我们会在之后的核心语言中重点提到
NOTE: F1 来调出说明文档

其他有趣的功能

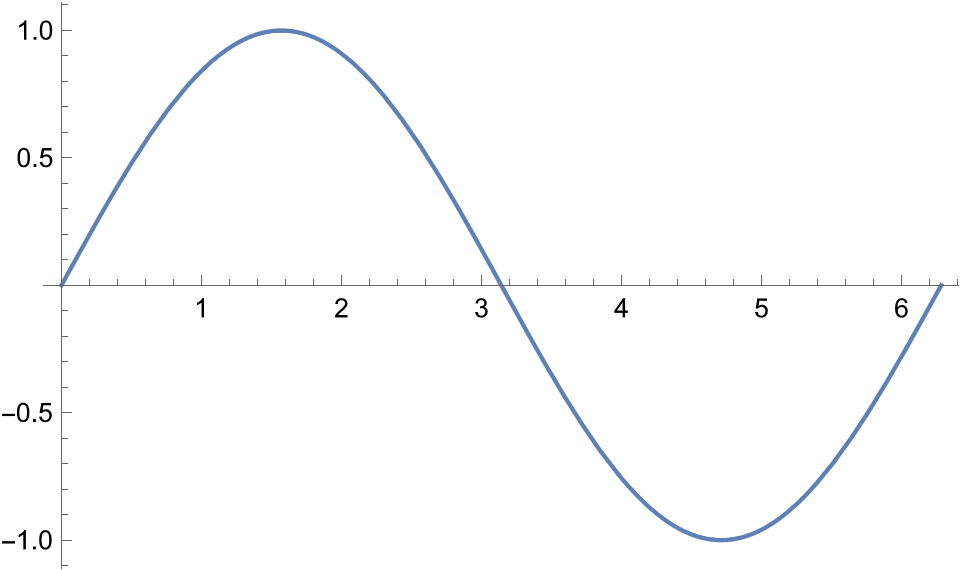
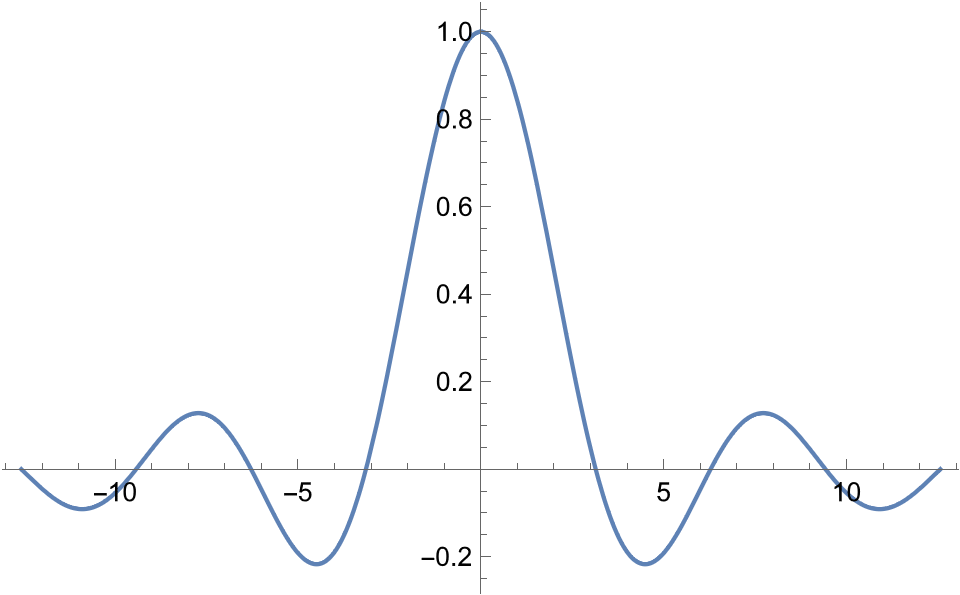
画图:

worksheet1_25.png

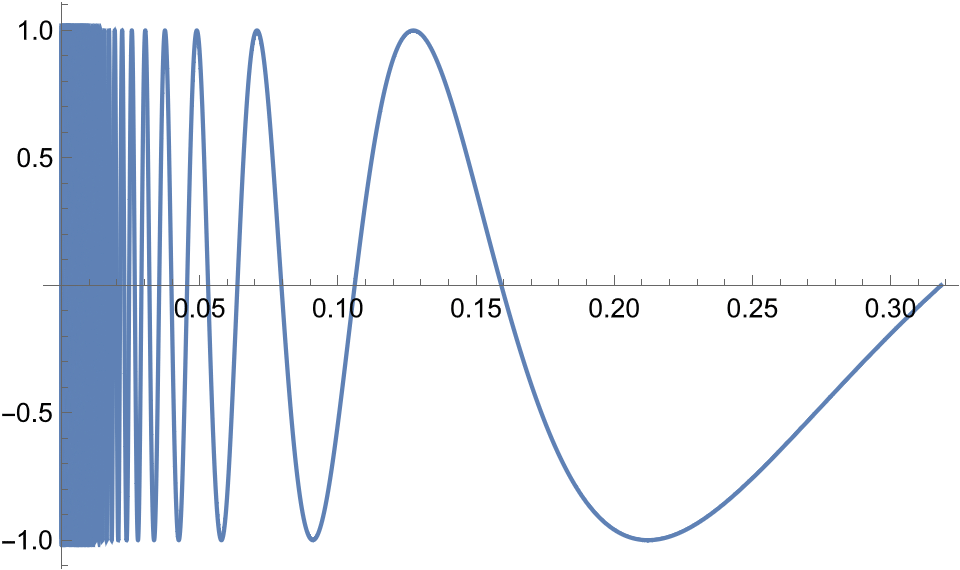
worksheet1_26.gif

NOTE: 可以通过 PlotPoints 属性来增加图像平滑程度

NOTE: Mathematica 由两部分组成 -- 前端与内核 (kernel), 你可以在工具栏中选择计算->退出内核, 来把之前的计算结果清空, 清理一些变量, 再给变量赋值之后, 变量名会由蓝色变为黑色.
NOTE: Mathematica 的注释为 (* *)

导入网站图片

worksheet1_27.png

worksheet1_28.gif

类似 PhotoShop 增加图像效果

worksheet1_29.png

worksheet1_30.gif

人脸识别

worksheet1_31.gif

worksheet1_32.gif

Mathematica 内置很多高级功能, 就像计算器一般, 只要你将参数正确输入, 就能实现在其他语言中很难实现的功能, 因此很适合快速功能的开发, 尽管效率可能不是很高

worksheet1_33.png

worksheet1_34.png

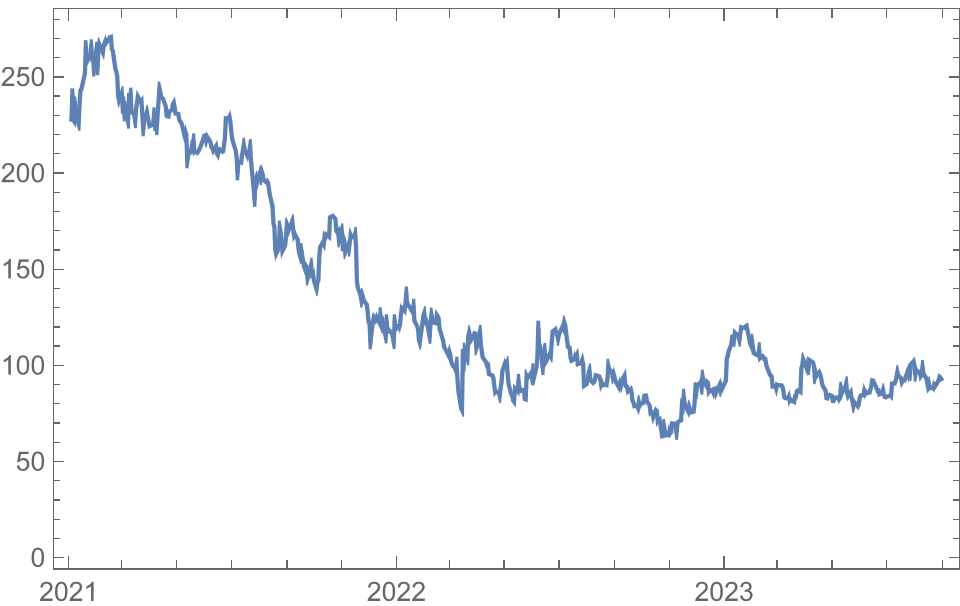
Mathematica 内部函数可以从互联网实时抓取数据

worksheet1_35.png

worksheet1_36.gif

值, 变量, 类型

上述简单的用法都不是 Mathematica 最核心的用法, 下面开始介绍核心语言.

我们先从和其他语言相似的部分讲起, 以下三种对象称为原子 (atom):

符号 (Symbol): 由字母和数字 (数字不能在起始位置) 构成的有限序列

数字 (Number): 整数, 有理数, 实数, 复数, (四元数)

字符串 (String): 由双引号 “” 括起来的任意字符构成的有限序列

符号可以认为是其他语言中的变量, 数字和字符串则是变量的值

Mathematica 变量不是类似 C 语言的强类型变量, 是类似 Python 和 R 的可变类型

worksheet1_37.png

worksheet1_38.png

worksheet1_39.png

worksheet1_40.png

命名变量时需要避开系统内建符号:

由第一个字母大写的单词组成（Camel命名法）：True、False、FactorInteger、SetAttributes

用来做判断的函数末尾通常有“Q”：EvenQ、PrimeQ、MatchQ

用人名命名的符号=人名+符号名：EulerGamma、BesselJ、DiracDelta

一种比较好的做法是在命名自定义符号时将首字母取为小写字母 (camel命名法), 也可以直接用中文命名, 但不推荐. 并且注意全角和半角.

类型检查问题：

worksheet1_41.png

worksheet1_42.gif

worksheet1_43.png

worksheet1_44.png

一个编程语言的类型检查越严格，程序员受到的束缚就越大。Mathematica 程序通常来说都比较短小，靠程序员自觉检查类型基本上就足够了，所以不需要太严格的类型检查机制。一个较弱的类型系统可以让程序员写出更灵活的程序。例如在上面的例子中，我们可以在需要的时候将 Sin[ ] 中的自变量（此时是个字符串）再替换为合法的数值，由此得到数学上有意义的结果

worksheet1_45.png

worksheet1_46.png

控制流

在 C 或者 Pascal 这种面向过程的结构化程序语言中，条件、循环和子程序是最基本的三种结构。有了这三种结构就可以实现一切算法。但是，在 Mathematica 程序中，条件和循环结构其实用得并不多。这是因为条件结构的功能基本上可以通过核心语言中的模式匹配来完成；而循环结构的功能则可以通过表处理和泛函编程完成。等读者熟悉这些核心语言的概念之后，会发现它们比条件和循环结构更灵活、更强大、并且更快。在本节中，为了让熟悉 C 语言的读者比较快地上手，我们简单地介绍一下 Mathematica 中的这些结构。

简单条件判断

worksheet1_47.png

worksheet1_48.png

worksheet1_49.png

worksheet1_50.png

worksheet1_51.png

worksheet1_52.png

worksheet1_53.png

worksheet1_54.png

多重条件判断

worksheet1_55.png

worksheet1_56.png

worksheet1_57.png

worksheet1_58.gif

worksheet1_59.png

worksheet1_60.png

简单循环

worksheet1_61.png

worksheet1_62.png

worksheet1_63.png

worksheet1_64.png

worksheet1_65.png

worksheet1_66.png

worksheet1_67.png

worksheet1_68.png

worksheet1_69.png

worksheet1_70.png

worksheet1_71.png

worksheet1_72.png

worksheet1_73.png

worksheet1_74.png

worksheet1_75.png

worksheet1_76.png

worksheet1_77.png

worksheet1_78.png

worksheet1_79.png

worksheet1_80.png

worksheet1_81.png

worksheet1_82.png

worksheet1_83.png

worksheet1_84.png

worksheet1_85.png

worksheet1_86.png

worksheet1_87.png

worksheet1_88.png

worksheet1_89.png

worksheet1_90.png

worksheet1_91.png

worksheet1_92.png

worksheet1_93.png

worksheet1_94.png

worksheet1_95.png

worksheet1_96.png

worksheet1_97.png

复杂循环

worksheet1_98.png

worksheet1_99.png

worksheet1_100.png

worksheet1_101.png

worksheet1_102.png

worksheet1_103.png

worksheet1_104.png

worksheet1_105.png

worksheet1_106.png

worksheet1_107.png

worksheet1_108.png

worksheet1_109.png

worksheet1_110.png

worksheet1_111.png

worksheet1_112.png

不推荐使用的：Break、Continue、Return、Goto。

函数

函数定义方法一：模式匹配+延迟赋值

worksheet1_113.gif

函数定义方法二：纯函数（λ-表达式、匿名函数）

worksheet1_114.gif

NOTE: 建议初学者使用方法二的完整形式，因为比较简单易懂。

例子: 求不大于给定正整数 n 的所有素数的和

worksheet1_115.png

worksheet1_116.png

worksheet1_117.png

worksheet1_118.png

Created with the Wolfram Language